参考资料：

生成网络简史

需要预备一些无监督学习的基础知识：

聚类，降维（例如 PC），特征学习，密度估计

生成模型：给定训练集，产生与训练集同分布的新样本。希望学到一个模型 $$ p_{model}(x)$$，其与训练样本的分布 $$ p_{data}(x)$$相近。

🍀：无监督学习的一个核心问题——密度估计问题

生成网络的分类：

显式密度估计
- 密度函数可解
  - NADE
  - MADE
  - PixelRNN/PixelCNN
- 密度函数可以近似
  - 变分自编码器 VAE
  - 马尔科夫链
隐式密度估计
- GAN

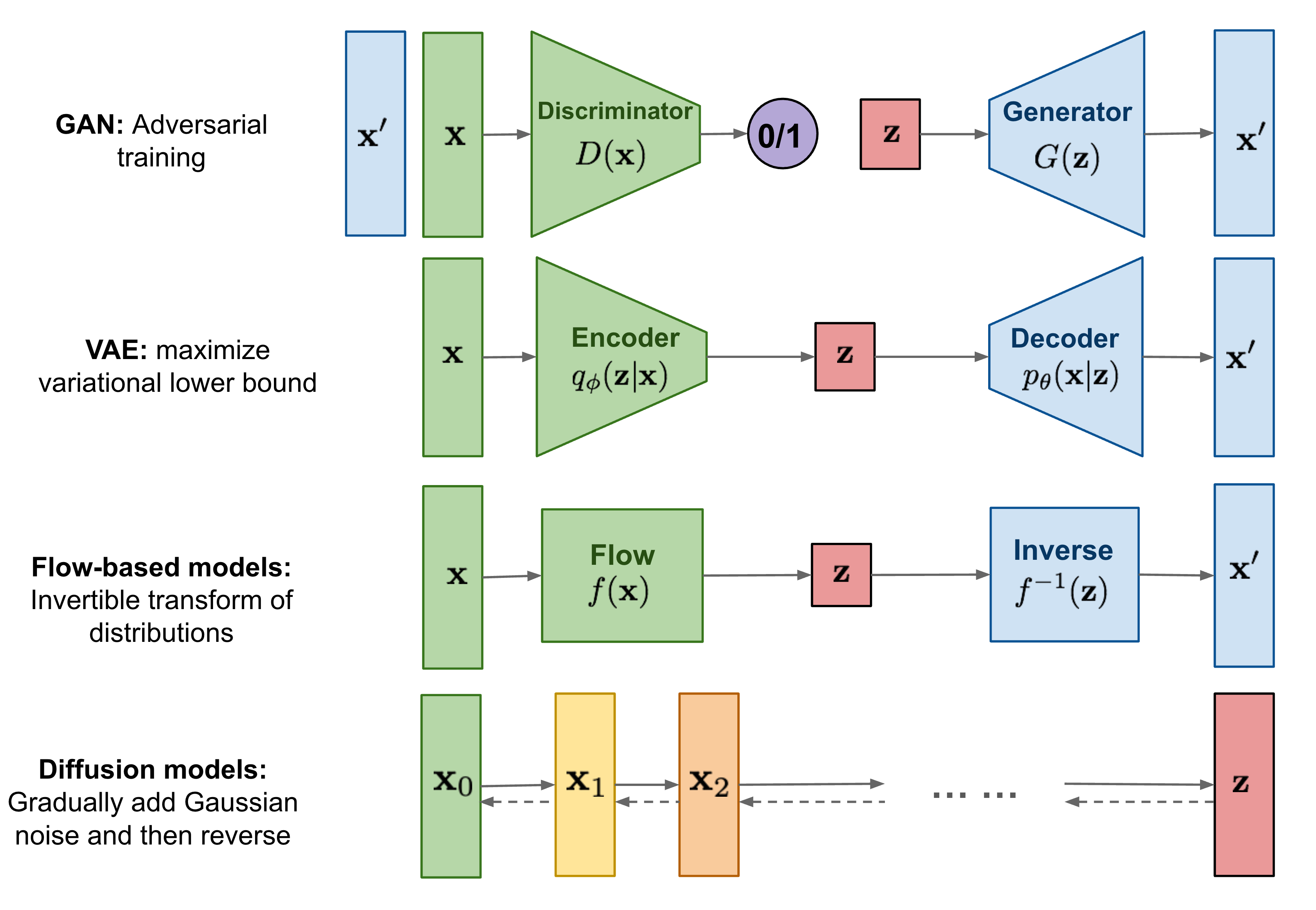
GAN

简介

Generative Adversarial Network，中文全称生成对抗网络，有两个神经网络作为主要部分——生成器（Generator）和判别器（Discriminator）。GAN的基本思想是通过让生成器和判别器相互对抗的方式来学习数据的分布特征。

对于图片而言（GAN可以用于合成多种类型的数据，不只是图片），生成器负责按照给定的描述来生成图片，而判别器会接受两种图片——真实图片和由生成器生成的图片。判别器会尝试区分这两种图片（无监督，事先不知道图片真假）。生成器和判别器在训练过程中相互竞争、相互改进，最终生成器学会生成逼真的数据，使得判别器难以区分真实数据和生成数据。

这么做的理由是，由于神经网络，尤其是卷积神经网络前期的不断发展，已经可以有效地对图片进行区分（分类），那么我们用这个已经成熟的神经网络，来为另一个不成熟的神经网络（生成器）计算“损失”，就有可能大大降低依靠人力来区分图片真假的成本，使得构建一个高效的生成网络成为可能。

GAN 在图像生成、图像转换、风格迁移等任务上取得了很好的效果，并且被广泛应用于计算机视觉和图像处理领域。这种网络结构的创新性在于，它能够学习到数据的分布，而不需要显式地定义数据的概率分布函数。

🍅 应用案例：早期的 WaifuLab 和 Crypko 就是采用 GAN 来生成插画的

原理推导

生成对抗网络其实是两个网络的组合：生成网络（Generator）负责生成模拟数据；判别网络Discriminator）负责判断输入的数据是真实的还是生成的。生成网络要不断优化自己生成的数据让判别网络判断不出来，判别网络也要优化自己让自己判断得更准确。二者关系形成对抗，因此叫对抗网络。

这是一个生成器和判别器博弈的过程。生成器生成假数据，然后将生成的假数据和真数据都输入判别器，判别器要判断出哪些是真的哪些是假的。判别器第一次判别出来的肯定有很大的误差，然后我们根据误差来优化判别器。现在判别器水平提高了，生成器生成的数据很难再骗过判别器了，所以我们得反过来优化生成器，之后生成器水平提高了，然后反过来继续训练判别器，判别器水平又提高了，再反过来训练生成器，就这样循环往复，直到达到纳什均衡。

生成网络的损失函数：
$$
L_{G}=H(1,D(G(z)))
$$
上式中，G 代表生成网络，D 代表判别网络，H 代表交叉熵，z 是输入随机数据。 $$D(G(z))$$ 是对生成数据的判断概率，1 代表数据绝对真实，0 代表数据绝对虚假。 $$H(1,D(G(z)))$$ 代表判断结果与1的距离。显然生成网络想取得良好的效果，那就要做到，让判别器将生成数据判别为真数据（即D(G(z))与1的距离越小越好）。

判别网络的损失函数：
$$
L_{D}=H(1,D(x))+H(0,D(G(z)))
$$
上式中，是真实数据，这里要注意的是，代表真实数据与1的距离，代表生成数据与0的距离。显然，判别器要想取得良好的效果，那么就要做到，在它眼里，真实数据就是真实数据，生成数据就是虚假数据（即真实数据与1的距离小，生成数据与0的距离小）。

生成网络和判别网络有了损失函数，就可以基于各自的损失函数，利用误差反向传播（Backpropagation）算法和最优化方法(如梯度下降法)来实现参数的调整，不断提高生成网络和判别网络的性能。

GAN 的缺点

GAN 的弱点也比较明显。如果判别器比较强，无论生成器怎样调整数据分布，判别器都能做出区分，网络就很难训练。

GAN 在业内以不稳定和难训练著称

VAE

简介

Variational Autoencoder，中文全称变分自编码器，是一种生成模型，也是一种无监督学习算法，用于学习数据的潜在表示和生成新的数据样本。与普通的自编码器（Autoencoder）不同，VAE引入了概率分布的概念，使得模型更加灵活。

VAE的基本思想是，将输入数据映射到一个潜在空间（latent space），并且在这个潜在空间中引入概率分布，通常是多变量高斯分布。VAE的网络结构分为编码器（Encoder）和解码器（Decoder）。编码器将输入数据映射到潜在空间的均值和方差参数，解码器则从潜在空间的采样点重构出数据。

训练VAE的过程涉及到最大化数据的似然概率，同时最小化潜在表示与先验分布（通常是标准正态分布）之间的KL散度（Kullback-Leibler Divergence），以保持生成的数据具有一定的连续性和规律性。

VAE的特点之一是，它能够学习数据的潜在结构，并且可以用于生成新的数据样本。与GAN不同，VAE生成的图像通常更加模糊，但它具有更好的潜在空间插值性质，即在潜在空间中，相似的点对应于相似的数据样本。这种特性使得VAE在某些应用中具有优势，例如生成具有连续变化特性的图像。

从自编码器到 VAE

名字里的 Auto 是“自己”的意思，不要误解为“自动”

🍩自编码器，无监督的特征学习，目的是利用无标签数据找到一个有效的低维特征提取器。

VAE 的前半部分——自动编码器，在之后整个生成网络的历史中，都发挥着巨大的作用。这是 VAE 的一项杰作。比如之前 HiNet 论文中进行特征融合，就是依靠编码器的部分来提取特征的。

编码器负责把图像转化为中间的表示形式，也就是我们常说的“潜空间”，Latent Space。之后解码器再负责把潜空间的特征，转化为人类可辨识的图片。

训练好的编码器可以接上一个分离器进行分类任务，需要微调编码器参数。这就是编码器特征提取的作用。

与之对应的，解码器则可以用于图像生成任务。

为什么需要 VAE？

如果只有先前的自编码器，我们无法生成没见过的图像。如果神经网络只见过满月和上弦月，那么中间几天的月相就无法生成。

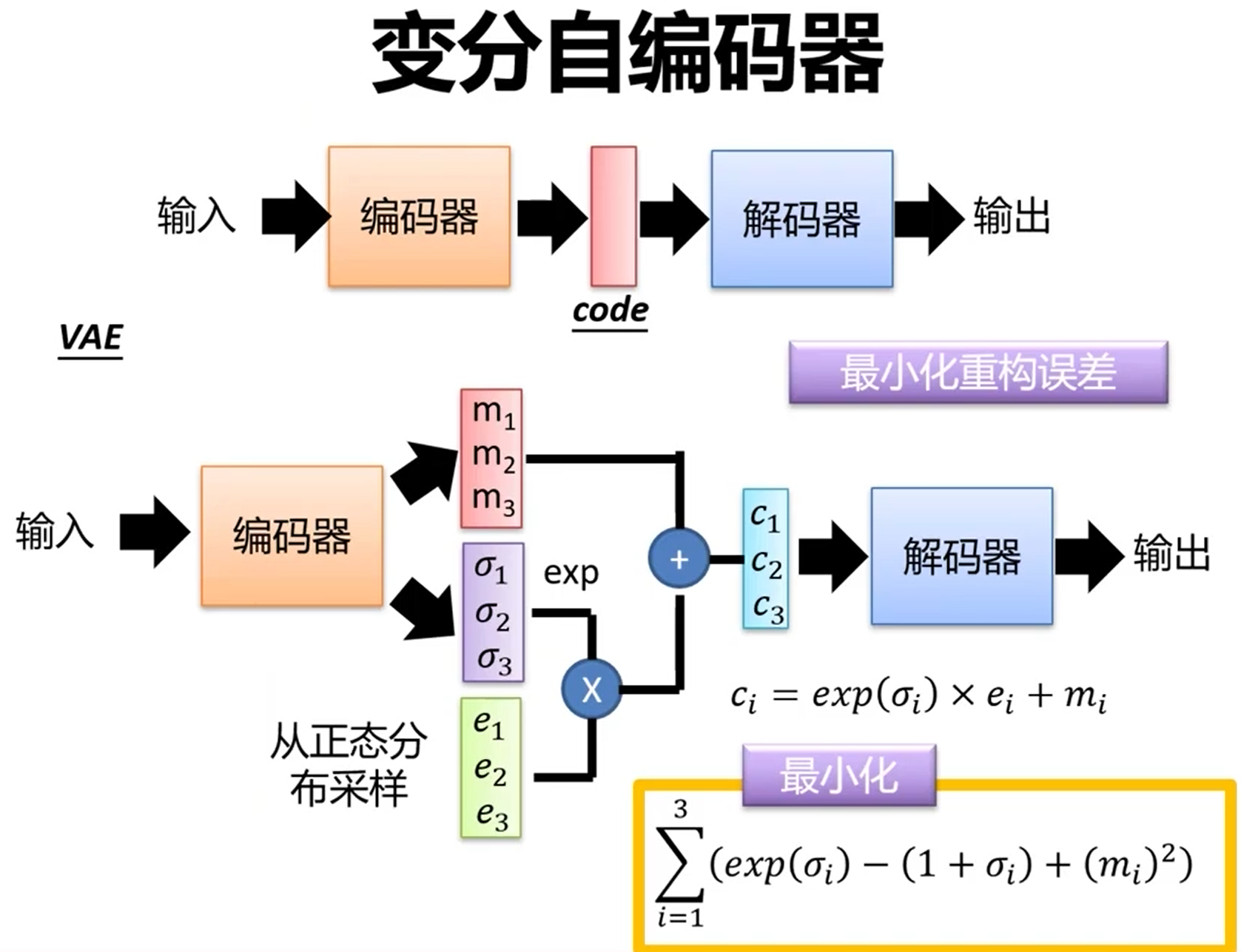
与直接对输入进行简单编码的自动编码器不同，VAE 的编码器在编码时不是仅仅生成特征向量，而是生成一个分布，包括均值（上图的e）和标准差（上图的 σ），此外还有一个高斯噪声（上图的 e）。特征向量的每一个数值都在这些分布中采样得到。

噪声的方差 σ 是从数据中学到的

高斯混合模型

用一系列高斯分布去逼近某个特定分布。

原理推导

原始的样本数据 $$x$$ 的概率分布：
$$
P(x)=∫
z

P(x)P(x∣z)dz
$$
假设 $$ z $$ 服从标准高斯分布，先验分布P ( x ∣ z ) 属于高斯分布，即 $$x ∣ z ∼ N ( μ ( z ) , σ ( z ) ) $$。其中，μ ( z ) 和σ ( z )是两个函数，分别是 $$z$$ 对应的高斯分布的均值和方差。
由于P ( z ) P(z)P(z)是已知的P ( x ∣ z ) P(x|z)P(x∣z)未知，所以求解问题实际上就是求μ ( z ) \mu(z)μ(z), σ ( z ) \sigma(z)σ(z)这两个函数。我们最开始的目标是求解P ( x ) P(x)P(x)，且我们希望P ( x ) P(x)P(x) 越大越好，这等价于求解关于x xx 最大对数似然：
$$
L=\sum_xlogP(x)
$$
logP(x)可变换为：
$$
l o g P ( x ) = ∫ z Q ( z ∣ x ) l o g P ( x ) d z
= ∫ z Q ( z ∣ x ) l o g P ( z , x ) P ( z ∣ x ) d z = ∫ z Q ( z ∣ x ) l o g ( P ( z , x ) Q ( z ∣ x ) Q ( z ∣ x ) P ( z ∣ x ) ) d z = ∫ z Q ( z ∣ x ) l o g ( P ( z , x ) Q ( z ∣ x ) ) d z + ∫ z Q ( z ∣ x ) l o g ( Q ( z ∣ x ) P ( z ∣ x ) ) d z = ∫ z Q ( z ∣ x ) l o g ( P ( x ∣ z ) P ( z ) Q ( z ∣ x ) ) d z + ∫ z Q ( z ∣ x ) l o g ( Q ( z ∣ x ) P ( z ∣ x ) ) d z = ∫ z Q ( z ∣ x ) l o g ( P ( x ∣ z ) P ( z ) Q ( z ∣ x ) ) d z + K L ( Q ( z ∣ x ) ∣ ∣ P ( z ∣ x ) )
$$
由于KL散度大于 0,可以得到：
$$
logP(x)⩾∫
z

Q(z∣x)log(
Q(z∣x)
P(x∣z)P(z)

)dz
$$
可得logP(x)下界:
$$
L
b

=∫
z

Q(z∣x)log(
Q(z∣x)
P(x∣z)P(z)

)dz
$$
原式可以表示为：
$$
logP(x)=L
b

+KL(Q(z∣x)∣∣P(z∣x))
$$
最小化KL散度

假设P(z)服从标准正太分布，且Q(z∣x)服从高斯分布$$ N(\mu,\sigma^2)$$,于是代入计算可得：

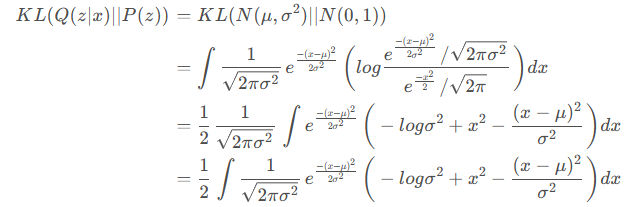
化简结果：
$$
KL(Q(z∣x)∣∣P(z))

=KL(N(μ,σ ^
2
)∣∣N(0,1))

1/2

(−logσ
2
+μ ^
2
+σ ^
2
−1)

VAE 本质上就是在我们常规的自编码器的基础上，对encoder的结果（在VAE中对应着计算均值的网络）加上了“高斯噪声”，使得结果decoder能够对噪声有鲁棒性；而那个额外的KL loss（目的是让均值为0，方差为1），事实上就是相当于对encoder的一个正则项，希望encoder出来的东西均有零均值。

另外一个encoder（对应着计算方差的网络）的作用是用来动态调节噪声的强度的。直觉上来想，当decoder还没有训练好时（重构误差远大于KL loss），就会适当降低噪声（KL loss增加），使得拟合起来容易一些（重构误差开始下降）；反之，如果decoder训练得还不错时（重构误差小于KL loss），这时候噪声就会增加（KL loss减少），使得拟合更加困难了（重构误差又开始增加），这时候decoder就要想办法提高它的生成能力了。

VAE 的进一步发展

VAE 通过输入和输出图片的相似程度（如 L1 距离）来计算损失，这样的损失更稳定，使得 VAE 的训练要比 GAN 可控许多。

这样训练出来的网络，就可以实现两个分布的相互转换（原空间和潜空间）。

🍇 这里的潜空间，是神经网络仅针对图片进行学习得出的，不与文字相挂钩，也是不可控的——人们只能根据重建图像来判断潜空间特征的好坏，却不清楚这究竟是一组什么特征。

如果需要让其可控，需要额外的网络接入来学习其潜空间表达，从而将文本描述也转化到潜空间，例如 Parti 网络。它使用了一个 transformer 来学习词语到潜空间的转换。在生成时，输入的词会首先被作为潜空间的样本，再通过解码器生成图像。

Parti: Pathways Autoregressive Text-to-Image Model (research.google)

这扩大了 VAE 的适用性，解码器不再是生成潜空间的特定样本，而是生成可能的样本分布，样本之后在这个分布中随机挑选出来。

🍊 应用案例：Dall-E 和 ERNIE-ViLG 都采用了 VAE 相关的模型。

总结一下，VAE 的思想就是，通过引入“随机性”，每一个样本对应的特征都可能略有不同（服从某个分布），这样就可以使得训练后的特征空间比较平滑，网络就有可能生成一些没有见过，但合理的输出。

生成网络笔记

生成网络简史

GAN

简介

原理推导

GAN 的缺点

VAE

简介

从自编码器到 VAE

为什么需要 VAE？

高斯混合模型

原理推导

化简结果：
$$
KL(Q(z∣x)∣∣P(z))

=KL(N(μ,σ ^
2
)∣∣N(0,1))

VAE 的进一步发展

标准化流

Diffusion models

生成网络简史

GAN

简介

原理推导

GAN 的缺点

VAE

简介

从自编码器到 VAE

为什么需要 VAE？

高斯混合模型

原理推导

化简结果：$$KL(Q(z∣x)∣∣P(z))​=KL(N(μ,σ ^2 )∣∣N(0,1))

VAE 的进一步发展

标准化流

Diffusion models

化简结果：
$$
KL(Q(z∣x)∣∣P(z))

=KL(N(μ,σ ^
2
)∣∣N(0,1))